linear algebra

Linear versus affine functions

ntthung Math

The term linear function has different meaning in calculus and in linear algebra, which often confuses me. Here’s the clarification, which is a note I made to myself.

In calculus, a linear function is a first degree polynomial: f(x) = ax + b. Obviously, the function is called linear because its graphical representation is a line. However, in linear algebra, this function does not have the linear properties. The notion linear function, or linear transformation, is a mapping that has the following properties:

\begin{array}{l c l l} f(x+y) &=& f(x) + f(y) & (1) \\ f(kx) &= & kf(x) & (2) \end{array}

In this context, f(x) = ax + b is not a linear function. To verify this, we check (1) and (2). On the left hand side,

\begin{array}{l c l} f(x+y) &=&a(x+y)+b\\ f(kx) &=&akx + b\end{array}

while on the right hand side,

\begin{array}{l c l c l}f(x) + f(y) &= &ax + b + ay + b &= &a(x + y) + 2b\\ kf(x) &= &k(ax+b) &= &akx + kb\end{array}

So both (1) and (2) are not satisfied, which shows that f(x) = ax + b is not a linear function. On the other hand, we can prove easily that f(x) = ax is a linear transformation.

The function f(x) = ax + b has another name: it is an affine function, which is a linear function plus a constant.

Note that a linear transformation preserves the origin (zero is mapped to zero) while an affine transformation does not. In other words, a linear function maps a straight light through the origin to another straight line through the origin (effectively, it makes a rotation with an angle a), while an affine function rotates the line by an angle $late a$ and translate it by a distance b.

In higher dimensions, what I’ve described still hold. x and b can be vectors in a vector space and a can be a matrix.

Okay, enough with the equations. Next, I’m just gonna playing with a few functions to give you some examples.

In Figure 1, the line x + y = 0 (black) is mapped to the red line with the linear transformation f(x) = 2x and to the blue line with the affine transformation f(x) = 2x + 3.

Linear_affine.PNG
Figure 1

In Figure 2, the same linear and affine transformations are applied to the curve y = x^3. Again, we see that the origin is preserved after the linear transformation but not the affine transformation.

Linear_affine_cubic.PNG
Figure 2

And finally, we apply the same transformations to a circle in Figure 3.

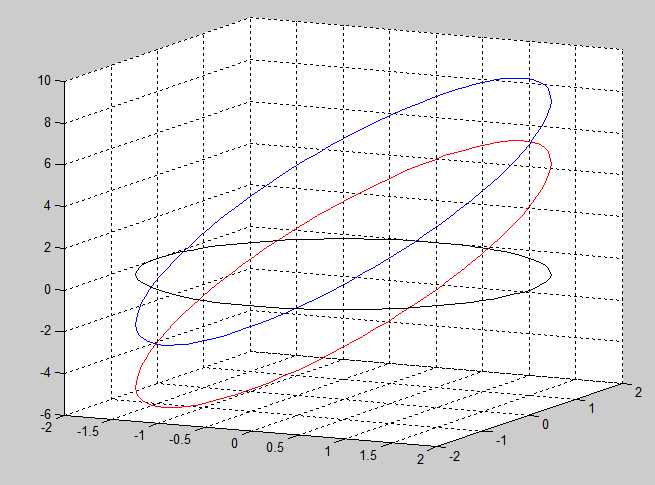
LInear_affine_circle.PNG
Figure 3

I think this is fun.